[…] La soluzione del problema del piano inclinato ebbe una notevole importanza nell'elaborazione della legge della caduta dei gravi da parte di Galileo.

L'opera di Galileo ci dà la possibilità di riconsiderare la distinzione tra moto perpetuo e motore perpetuo: il significato della legge d'inerzia è che un corpo non si può mettere in moto da solo e che, una volta in moto non può distruggere il proprio moto. Una resistenza deve essergli opposta, tramite la quale il moto del corpo viene assorbito da altri corpi. Pertanto la possibilità di un corpo di restare indefinitamente in moto è legata alla impossibilità di compiere lavoro durante il moto, cioè all'impossibilità di una continua produzione di lavoro. La legge d'inerzia è dunque strettamente collegata all'impossibilità del motore perpetuo e Galileo ne era ben consapevole: tale impossibilità infatti sarà alla base della scoperta della legge di caduta dei gravi.

Anche le leggi del piano inclinato (Stevino), hanno un ruolo nella sperimentazione che conduce Galileo a formulare la legge di caduta dei gravi. Galileo misura i tempi di caduta con un orologio ad acqua e scopre che le distanze percorse sono proporzionali al quadrato dei tempi impiegati a percorrerle:

s=1/2 gt 2

Le velocità finali sono proporzionali al tempo:

v f =g t

Ma l'idea di Galileo che sarà fondamentale per lo sviluppo del principio di conservazione dell'energia è la seguente: le velocità finali di caduta sono indipendenti dalla traiettoria percorsa (cioè dall'inclinazione del piano) e dipendono solo dall'altezza di caduta.

Sulla base di questa idea Galileo determina che al variare dell'inclinazione del piano variano sia la costante di proporzionalità g sia il tempo t, ma il loro prodotto resta costante:

g't'=gt.

L'impossibilità del perpetuum mobile è di nuovo al centro dell'argomentazione. Galileo suppone che un corpo acquisti la stessa velocità finale sia cadendo secondo l'altezza del piano inclinato, sia cadendo secondo la lunghezza dello stesso piano. Immaginiamo infatti di deviare la velocità finale verso l'alto: il movimento sarà speculare e la velocità diminuirà proporzionalmente al tempo, annullandosi all'altezza originaria di caduta.

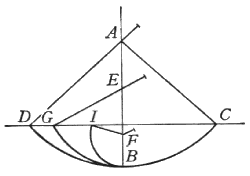
Fig.7 Pendolo con vincoli di Galileo

Fig. 8 Successioni di piani inclinati

Il corpo infatti risale alla stessa altezza da cui è caduto: se l'altezza fosse superiore sarebbe violata l'impossibilità del perpetuum mobile; il corpo, con operazioni successive, in virtù del solo proprio peso potrebbe essere sollevato indefinitamente. Questa considerazione teorica porta a fissare l'attenzione sull'altezza di caduta e non sulla traiettoria percorsa. Galileo formula anche una indicazione sperimentale.

Spostato il pendolo dalla sua posizione di equilibrio e lasciatolo cadere, esso risale alla stessa altezza dall'altra parte. Il movimento della sfera del pendolo lungo il suo arco di cerchio può essere considerato come una caduta su una serie di piani con differente inclinazione. Si può facilmente, dice Galileo, far risalire il corpo su un diverso arco di cerchio, cioè su una diversa serie di piani inclinati. Ciò viene realizzato mediante i chiodi f, g, h. Si può controllare che l'altezza di risalita è sempre la stessa, indipendentemente dalla traiettoria. Nel caso in cui la lunghezza del filo non consenta di raggiungere la posizione di risalita (vincolo h) il corpo tende a riavvolgersi sul vincolo, indice che la velocità non si è annullata.

Questo fondamentale risultato porta alla nota legge:

v f = Ö2gh

[…]

(capitolo II)

[…] Un ampliamento essenziale all'idea dell'eterno divenire venne apportato dall'introduzione della legge dell'inerzia. L'antica opinione, la quale poneva la velocità proporzionale alla forza e quindi, anche in assenza di qualsiasi resistenza, considerava estinto con la forza anche il moto venne a poco a poco lasciata cadere, già nel XVI secolo, dai più autorevoli fisici. Nicola Cusano, Leonardo da Vinci e Benedetti, presso i quali già ritroviamo alcune inconsapevoli applicazioni del non ancora chiaramente intuito principio d'inerzia, rappresentano i più importanti precursori di Galilei, il quale per primo (1638) enunciò in forma definita il principio[4]. Più tardi, specialmente Cartesio e Newton hanno contribuito a che il principio raggiungesse un'importanza fondamentale per la meccanica. […]

[4] Discorsi e dimostrazioni matematiche, Dialogo terzo: " Dal che segue in pari modo anche il moto in orizzontale essere eterno: se infatti è uniforme esso non si indebolisce o diminuisce e tanto meno si accresce." [in latino nel testo]

(Capitolo V)

[…] L'equivalenza tra causa ed effetto si manifesta, secondo Leibniz, nel fatto che un sistema, nelle condizioni che corrispondono alla causa ed all'effetto, contiene continuamente la stessa quantità di energia. In questa ipotesi risiede la grande importanza del principio, per lo sviluppo dell'energetica. Che ora l'effetto non possa essere maggiore della causa, risulta, come intende Leibniz, dall'impossibilità di un perpetuum mobile, il quale consisterebbe appunto in una superiorità dell'energia dell'effetto rispetto a quella della causa. Che d'altra parte l'effetto totale non possa essere minore della causa, non viene ulteriormente dedotto. Leibniz accenna ancora espressamente al fatto che le eccezioni osservabili alla legge sono solo apparenti; infatti, quand'anche una parte dell'energia venisse assorbita dagli ostacoli, essa non sarebbe stata distrutta, ma solo trasferita negli ostacoli. Una dimostrazione più rigorosa del principio di uguaglianza non viene dunque fornita da Leibniz e, a suo parere, non è affatto possibile. Infatti egli considera questo principio come un assioma, alla stessa stregua della tesi dell'impossibilità del moto perpetuo; che l'effetto totale sia continuamente uguale alla causa piena, sarebbe essenzialmente un'ipotesi dell'alta metafisica, la quale non si diffonderebbe in vuote parole ma tratterebbe l'essenziale ed il comprensibile delle cose.

Due corollari, ai quali secondo Leibniz conduce il principio di uguaglianza, sono interessanti, in quanto essi rappresentano le generalizzazioni filosofico naturali di due teoremi fisico-matematici i quali furono di grande importanza per lo sviluppo dell'energetica. Uno dei due è il teorema di Galilei, che si riferisce alla caduta obliqua da una data altezza ed afferma l'indipendenza della velocità così raggiunta dalla forma della traiettoria il secondo è la tesi di Huygens, che stabilisce l'uguaglianza tra l'effettivo moto in discesa ed il possibile moto in salita. […]

(Capitolo VIII)

[…] La stretta interdipendenza che in tutti i tempi legò la meccanica, dalla quale cominciarono ad evolversi le teorie energetiche, alla matematica, ebbe come conseguenza che fin dagli inizi della fisica moderna il perfezionamento delle idee di filosofia della natura, riunite nella legge della conservazione della forza, fu accompagnato da uno sviluppo parallelo delle idee teoreticomeccaniche, la cui configurazione in estensione e compendio costituì il primo fondamento matematico per la nuova energetica.

Gli inizi di questa evoluzione risalgono fino a Galilei. Egli è il creatore di due principi i quali già racchiudono in sè i germi di due importanti teoremi dell'energetica moderna e che egli enunciò per primo nei suoi Discorsi (1638). Le osservazioni sulla caduta lungo il piano inclinato condussero Galilei all'importante nozione che per cadute da uguale altezza la velocità finale del corpo in caduta sarebbe indipendente dalla lunghezza della traiettoria descritta e quindi anche dall'inclinazione del piano[1]. Le considerazioni sul piano inclinato convinsero anche Galilei dell'ideale reversibilità di ogni processo meccanico; per evidenziarla egli partì dal semplice esempio del moto del pendolo.

Se B è il punto più basso della traiettoria del pendolo possiamo concludere con certezza, secondo Galilei, che la velocità raggiunta nel punto B da una sfera che cada lungo l'arco CB, sarebbe sufficiente a provocare un movimento in su, lungo un arco BD di uguale lunghezza, fino ad un'uguale altezza[2]. L'analogo deve naturalmente valere per l'energia, per la forza, che Galilei denomina momento. Quindi, il momento prodotto dalla caduta lungo l'arco BD dovrebbe essere uguale al momento che muove lo stesso corpo in su da B a D, sicché dunque, in generale, ogni momento prodotto dalla caduta sarebbe uguale al momento che è in grado di risollevare il corpo lungo il medesimo arco[3].

Ponendo ora in relazione queste considerazioni con il principio discusso prima, Galilei riuscì a generalizzarle anche per un moto che si svolga su un sistema di quanti si vogliano piani, diversamente inclinati. Se si eliminassero gli ostacoli che in un moto del genere si oppongono all'esperimento, apparirebbe ben chiaro, come intende Galilei, che la forza, la quale racchiude in sè l'effetto della caduta, sarebbe altresì in grado di riportare i corpi all'altezza da cui sono caduti[4]. […]

[1] Discorsi e demostrazioni matematiche, Dialogo terzo, "De moto naturaliter accelerato": "Assumo che i livelli di velocità acquisiti dal medesimo mobile su diverse inclinazioni dei piani siano sempre uguali, quando le elevazioni degli stessi piani siano uguali."[in latino nel testo]

[2] ib.: "Dalche possiamo veracemente concludere, che l'impeto acquistato nel punto B dalla palla nello scendere per l'arco CB, fù tanto che bastò a risospingersi per un simile arco BD alla medesima altezza."[in italiano nel testo]

[3] ib.: "adunque anco il momento acquistato nella scesa DB, è eguale à quello, che sospigne l'istesso mobile per il medesimo arco da B in D, si che universalmente ogni momento acquistato per la scesa d'un arco è eguale à quello, che può far risalire l'istesso mobile per il medesimo arco."[in italiano nel testo]

[4] ib.: "Mà levato l'intoppo, che progiudica all'esperienza, mi par bene, che l'inteletto resti capace, che l'impeto (che in effetto piglia vigore dalla quantità della scesa) sarebbe potente à ricondurre il mobile alla medesima altezza."[in italiano nel testo]

(Capitolo 1)

[…] Anche G. Galilei sembra essere partito da una premessa analoga a quella di Stevin nella dimostrazione della tesi che la velocità raggiunta da un grave nella caduta lungo una traiettoria qualsiasi dipende solo dalla distanza verticale tra le posizioni iniziale e finale, assumendo che, se questo principio non fosse esatto, si potrebbe subito indicare un mezzo per portare un corpo ad una altezza maggiore solo per effetto del proprio peso, facendolo cadere lungo una certa linea curva e risalire di nuovo lungo un'altra [linea curva n.d.t.] appropriata; in tal modo avremmo naturalmente ottenuto il perpetuum mobile.

In stretto rapporto con ciò sta la nozione, uguamente già acquisita da Galilei, che, se si solleva (lentamente) (v8) un carico maggiore mediante un peso in caduta, i prodotti dei pesi per le traiettorie contemporaneamente percorse sono uguali, proposizione che più tardi venne ampliata, specialmente da Joh. Bernoulli (5) (1717) come principio degli spostamenti (velocità) virtuali. Proprio la tesi che un corpo non può salire in virtù del proprio peso o, in termini più generali, che un sistema di punti o corpi pesanti non può, per mezzo della forza motrice del suo peso, salire più alto del suo centro di gravità è diventata della massima importanza per lo sviluppo della meccanica ad opera di C. Huygens. […]